TL;DR. To prevent potential unfavorable scenario reported by Sam (outlined below in Potential Attack Scenario), the new update on Alpha Homora will

1) use price oracle as a solution to enable leverage function on IndexCoop pool
2) lower leverage 3x -> 2.5x on 4 Uniswap pools
3) re-enable leverage at 1.75x on IndexCoop pool

These updates make the potential scenario to not be profitable anymore and provide a larger liquidation buffer for users. See below for details on how we derive our solutions and rationale in choosing specific parameters.

Note there are more new features that we are launching tomorrow, so stay tuned for more updates from us!

On Saturday October 10th, Alpha team worked with PeckShield team and Sam (@samczsun) to come up with a solution to address a potential scenario (outlined below in Potential Attack Scenario). Although this scenario is very unlikely because the attacker’s capital is at risk of being front-runned or arbitraged by others, we decided to disable debt issuance on WETH/DPI pool since Saturday and have come up with a solution to still enable leverage on WETH/DPI pool while ensuring this unfavorable scenario won’t happen.

Potential Attack Scenario (a simplified version)

The original attack presented by Sam is much more sophisticated than the one below, requiring a deep understanding of the strategy smart contract.

TL;DR. Pump -> Open a position -> Dump -> Liquidate.

Here’s a step-by-step summary of the simplified attack vector (on WETH/DPI pair):

1. Dump ETH to WETH/DPI pool.
   Effect: DPI-per-ETH price significantly rises.
2. Open a position when DPI/ETH price is very high.
   Effect: DPI-per-ETH price rises even more (due to roughly half-swapping ETH to DPI).
3. Buy back the dumped ETH using DPI.
   Effect: Get higher DPI-to-ETH rate due pumped price from step 2.
4. (Optional) Liquidate the opened position to gain extra 5% of the position value.
   Effect: Attacker profits slightly more.

The questions we’ll analyze include:

• How much capital is needed in step 1 to perform such an attack?
• How much can the attacker net gain?
• What are the attacker’s risks?
• How can we mitigate or prevent this kind of attack?

An Example Scenario

For the sake of simplicity, we assume 0% swap fee (attacker gains more).

Let’s look at the following example scenario:

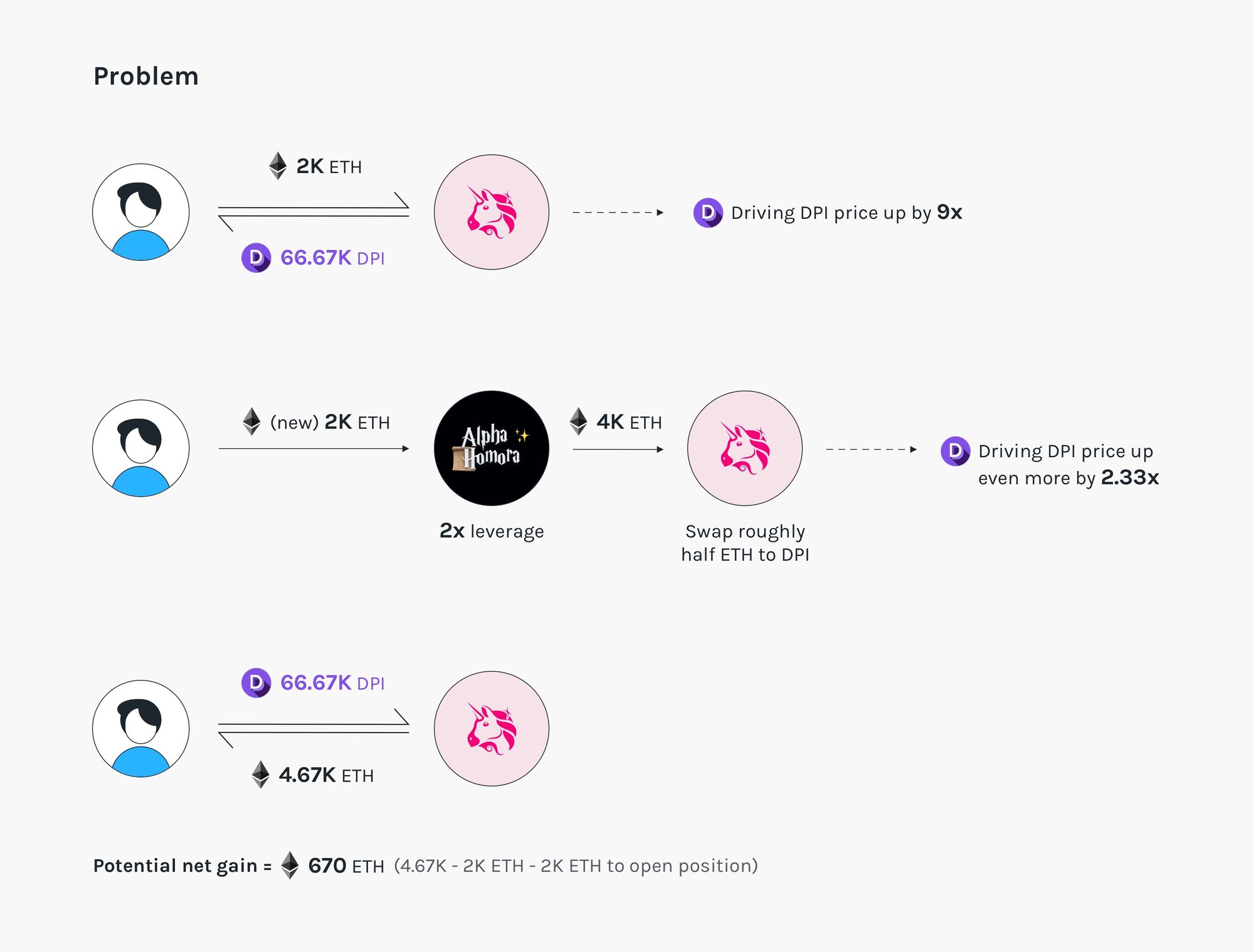
Assume the pool initially has 1k ETH + 100k DPI. The DPI/ETH spot price is 0.01.

1. Attacker swaps in 2k ETH, receiving 66.67k DPI.
   Effect: The pool now has 3k ETH + 33.33k DPI. The DPI/ETH spot price becomes 3k/33.33k = 0.09.
2. Attacker opens a position by supplying 2k ETH and borrowing 2k ETH from the bank, leveraging at 2x times. The protocol swaps roughly half of the ETH and supplies liquidity to the pool.
   Effect 1: The pool now has 7k ETH + 33.33k DPI. The DPI/ETH spot price becomes 0.21.
   Effect 2: The attacker holds roughly \(\sqrt{7k \cdot 33.33k} - \sqrt{1k \cdot 100k} \approx 5264\)  LP shares.
3. Attacker swaps in 66.67k DPI from step 1, gaining a total of 4.67k ETH.
   Effect 1: The pool now has 2.33k ETH + 100k DPI.
   Effect 2: The position is now worth roughly 1600 ETH.
4. (Optional) Attacker liquidates the opened position (if at risk), gaining roughly \(5\% \cdot 1600 \approx 80 \) ETH

Attacker’s ETH required capital: 4k.
Attacker’s ETH gain: 4.67k + 80.
Attacker’s ETH net gain (gain - capital): 750.

A Generalized Scenario

Here's a more generalized scenario.

Assume the pool initially has \(A\) ETH + \(B\) DPI. The DPI/ETH spot price is \(\frac{A}{B}\).

1. Attacker swaps in \(X\) ETH, receiving \(\frac{BX}{X+A}\) DPI.
   Effect: The pool now has \((A+X)\) ETH + \(\frac{AB}{A+X}\) DPI. The DPI/ETH spot price becomes \(\frac{(A+X)^2}{AB}\).
2. Attacker opens a position by supplying \(Y\) ETH and borrowing \(Z\) ETH from the bank, leveraging at \(\frac{Y+Z}{Y}\) times. The protocol swaps roughly half of the ETH and supply liquidity to the pool.
   Effect 1: The pool now has \((A+X+Y+Z)\) ETH + \(\frac{AB}{A+X}\) DPI. The DPI/ETH spot price becomes \(\frac{(A+X)\cdot(A+X+Y+Z)}{AB}\).
   Effect 2: The attacker holds roughly \(L = \sqrt{(A+X+Y+Z)\cdot\frac{AB}{A+X}} - \sqrt{(A+X)\cdot\frac{AB}{A+X}}\) LP shares.
3. Attacker swaps in \(\frac{BX}{X+A}\) DPI from step 1, gaining \(X + \frac{X(Y+Z)}{A+X}\) ETH.
   Effect 1: The pool now has \((A + \frac{A}{A+X}\cdot (Y+Z))\) ETH + \(B\) DPI.
   Effect 2: The position is now worth roughly \(2\cdot L \cdot \sqrt{\frac{A + \frac{A}{A+X}\cdot (Y+Z)}{B}} \) ETH.
4. (Optional) Attacker liquidates the opened position (if at risk), gaining roughly \(F \cdot 2\cdot L \cdot \sqrt{\frac{A + \frac{A}{A+X}\cdot (Y+Z)}{B}} \) ETH, where \(F\) is the killFactor (currently at \(F = 5\%\)).

Attacker’s ETH required capital: \(X + Y\).
Attacker’s ETH gain: \(X + \frac{X(Y+Z)}{A+X} + 2FL\sqrt{\frac{A + \frac{A}{A+X}\cdot (Y+Z)}{B}}  \).
Attacker’s ETH net gain (gain - capital): \( \frac{XZ - AY}{A+X} + 2FL\sqrt{\frac{A + \frac{A}{A+X}\cdot (Y+Z)}{B}} \).

So, how much can the attacker net gain in simpler terms? Let's simplify and upperbound the above expression.

Upper-bounding the Attacker's Net Gain

Suppose that the protocol allows leverage up to \(K\) times (with \(K\le 3\) currently). This means the attacker can only borrow up to \((K-1)\) times the supplied ETH, i.e., \(Z \le (K-1)Y\). The first term is then \(\frac{XZ-AY}{A+X} \le \frac{(K-1)XY-AY}{A+X}\).

We simplify the second term in the expression:

$$\begin{aligned}&2FL\sqrt{\frac{A + \frac{A}{A+X}\cdot (Y+Z)}{B}} \\ &= 2F\left({\sqrt{(A+X+Y+Z)\frac{AB}{A+X}} - \sqrt{(A+X)\frac{AB}{A+X}}}\right) \sqrt{\frac{A(A+X+Y+Z)}{B(A+X)}} \\ &= 2F\left(\sqrt{A+X+Y+Z} - \sqrt{A+X}\right) \cdot \sqrt{\frac{AB}{A+X}}\cdot \sqrt{\frac{A(A+X+Y+Z)}{B(A+X)}} \\ &= 2F\left(\frac{Y+Z}{\sqrt{A+X+Y+Z} + \sqrt{A+X}}\right) \cdot \frac{A}{A+X} \cdot \sqrt{A+X+Y+Z} \\ &= 2F(Y+Z)\cdot \frac{A}{A+X}\cdot \frac{\sqrt{A+X+Y+Z}}{\sqrt{A+X+Y+Z} + \sqrt{A+X}} \\ &\le 2F(Y+Z)\cdot \frac{A}{A+X}\\ &\le 2F(Y+(K-1)Y) \cdot \frac{A}{A+X} \\ &= 2FKY \cdot \frac{A}{A+X} \end{aligned}$$

Combining the two terms, the attacker's net gain is upper-bounded by

$$\begin{aligned} &\frac{(K-1)XY-AY}{A+X}  + 2FKY \frac{A}{A+X} \\ &= \frac{Y}{A+X} \cdot \left((K-1)X - A + 2FK\cdot A\right) \\ &= \frac{Y}{A+X} \cdot \left((K-1)X - (1-2FK)\cdot A\right) \end{aligned} $$

Thus, the attacker will can start gaining when \((K-1)X \ge (1-2FK)\cdot A\), or \(X \ge \frac{1-2FK}{K-1}\cdot A\).

At 2x leverage (\(K = 2\)) and 5% liquidation bonus (\(F = 0.05\)), the attacker can start profiting when \(X \ge 0.8A\). So, the spot price after step 1 for the attack is \(\frac{(A+X)^2}{AB} \ge \frac{(A+0.8A)^2}{AB} = \frac{3.24A}{B}\), at least 3.24 times than the normal spot price.

At 3x leverage (\(K = 3\)) and 5% liquidation bonus (\(F = 0.05\)), the attacker can start profiting when \(X \ge 0.35A\), meaning the amount of attacker's required capital is roughly at least one-third of the pool's initial ETH amount. In this case, the skewed spot price after step 1 for the attack is \(\frac{(A+X)^2}{AB} \ge \frac{(A+0.35A)^2}{AB} = \frac{1.82A}{B}\), at least 1.82 times the normal spot price.

Attack Summary. The attack vector relies on Pump -> Open a position at a very bad price -> Dump. The attack can affect the ETH borrowed and thus the ETH lenders.

Attacker's Risk

The attacker has several risks if he/she decides to attack:

• For the 4 Uniswap pools (WETH/USDT, WETH/USDC, WETH/DAI, WETH/WBTC) with deep liquidity, the amount of resources required for the attack is in the order of ~300k ETH ($100M).
• For WETH/DPI pool, the attacker only requires the capital in the order of ~20k ETH ($7M). Even though it's not a small amount, we would like our protocol to be on the safer side from such risk of attack, so we decided to pause any action that can put Alpha Homora protocol at risk, i.e., debt issuance.
• Since our smart contract only allows calls from Externally Owned Account (EOA), or user addresses, this eliminates the risk from flash loans or a composed attack into a single transaction.
  
  Specifically, opening/liquidating a position requires a separate call from user addresses. If the attacker decides to attack, the steps 1 & 2 to skew Uniswap price would provide a huge arbitrage opportunity for monitoring bots or other users, i.e., the attacker is at a high risk of losing the invested capital for the attack.

Other Potential Attack Vectors

There are 2 ways an attack may obtain funds from the protocol:

1. Position Opening Attack. This kind of attack will be similar to the attack vector described in the above scenario (opening a position when Uniswap price is skewed).
2. Liquidation Attack. The attack essentially skews Uniswap price so positions close to liquidation threshold become liquidatable. The attacker can then liquidate those positions, and de-skews the Uniswap price back to normal. Basically, Pump-Liquidate-Dump mechanism, gaining liquidation bonus while paying swap fees.

Protocol Update

To mitigate potential attacks, we patch the update as follows:

1. Alpha Homora smart contract will only allow opening/liquidating the position when the Uniswap spot price is within a certain threshold of price reported by the price oracle.
2. Lower leverage to up to 2.5x and workFactor to 65% for the 4 Uniswap pools (WETH/WBTC, WETH/USDT, WETH/USDC, WETH/DAI).
3. Re-enable leverage on WETH/DPI pool up to 1.75x and lower workFactor to 50%.

The first update limits how much the spot price can be skewed when opening a position. Here's how the updated version of Alpha Homora will work:

• The oracle price will be median price reported by CoinMarketCap, CryptoCompare, and CoinGecko, and it will update every 1 day or when the off-chain price deviates by more than 5%.*
• The updated version of Alpha Homora will allow opening/liquidating a position only when the price difference between Uniswap spot price and median price is within 30% of the oracle price, capping spot Uniswap price to deviate at most 1.30x from the oracle price.

This limits the attacker's sandwich attack to temporarily fake Uniswap spot price by dumping assets and buying back those assets in the same transaction block.

*Note: The first version of price oracle will use these 3 sources. In the future updates, we may switch to price reports from decentralized price oracles e.g. Uniswap TWAP, Chainlink, Band, etc.

The second and the third updates provide more safety buffer against liquidation attack.

Note 1: Bad oracle price cannot steal users' funds, so even if initially the price oracle is managed by us, your funds are still SAFU.

Note 2: If the off-chain price is still within 5%, then there's no need for the price to sync on-chain (our analysis below takes into account the 5% offset already). So, we'll initially set sync-time to 1 day.

Protocol Update Analysis

So how can the updated version of Alpha Homora mitigate the attacks?

Recall that our price oracle is guaranteed to be within 1.05x of the off-chain market price and that the protocol only allows opening/liquidation a position only when the Uniswap spot price is within 1.30x threshold from the oracle price. So,

1. The attacker can only change the Uniswap price by at most \(1.05 \cdot 1.30 = \) 1.365x factor. The 1.365x price change factor translates to a position's health change of at most \(\sqrt{1.365} \approx \) 1.1683x factor, meaning the debt ratio can also change by at most 1.1683x factor.
   
   The attack would be reverted if the debt ratio after opening a position exceeds workFactor. So, together with a cap on debt ratio change, the position's worst possible debt ratio would still be healthy under killFactor (e.g., \(workFactor \cdot 1.1683 < killFactor\)).
   
   For the specific attack scenario above, the attacker would require minimum of 1.82x price change factor, which is now impossible with the new update.
2. For the 4 Uniswap pools, a position can be at risk of such liquidation attack when the position's debt ratio hits \(80\%/1.1683 \approx\) 68.47%.* Lowering the pools' leverage to 2.5x means the initial debt ratio will be roughly 60% (~1.30x price tolerance).
   
   For the WETH/DPI pool, a position can be at risk of such liquidation attack when the position's debt ratio hits \(60\%/1.1683 \approx\) 51.35%.* Lowering WETH/DPI leverage to 1.75x means the initial debt ratio will be roughly 42.9% (~1.43x price tolerance).

*Note: This is considering the worst case scenario. However, in practice, for the attacker to perform 1.365x price change factor, the amount of capital required would be ~16% of the ETH in the corresponding pool. The attack would lose 0.3% swap fees on both swap in and out on the 16% portion. Moreover, the onlyEOA modifier forces the attack to be split into multiple transactions, leaving the attacker's capital at high risk of getting arbitraged between the transactions.

This update essentially aims to patch the potential risk of manipulated-price attack. By using price oracle, Alpha Homora can ensure that the attacker can manipulate the Uniswap spot price only to a certain extent, which proves insufficient for the attacker to positively net gain (and so the protocol doesn't incur loss).

Future Updates

The current update relies on median price fed by 3 centralized resources, and we would like to transition to a more decentralized price oracle option (e.g., Uniswap Time-weighted average price, Chainlink, Band, etc.) in future updates.

About Alpha

Alpha Finance Lab is an ecosystem of DeFi products, starting on Binance Smart Chain and Ethereum. Alpha Finance Lab is focused on building an ecosystem of automated yield-maximizing Alpha products that interoperate to bring optimal alpha to users on a cross-chain level.

We are moving at a rapid pace, so we encourage everyone to join our Discord for the latest updates, follow us on Twitter, or read more about us on our Blog!